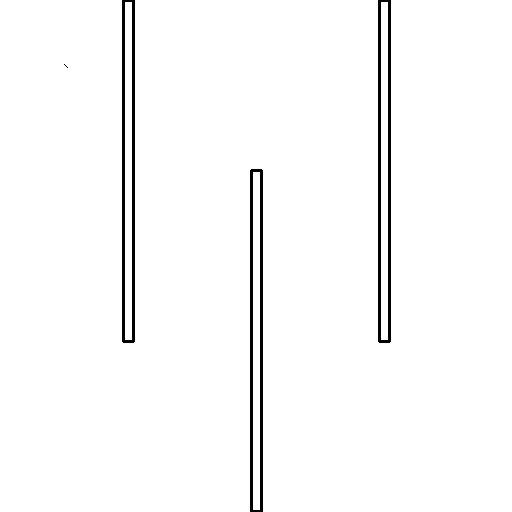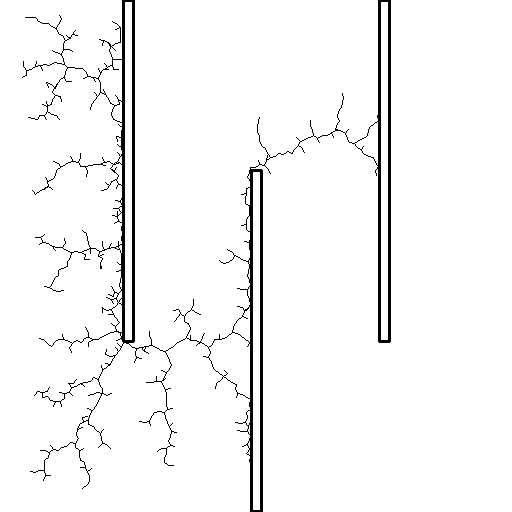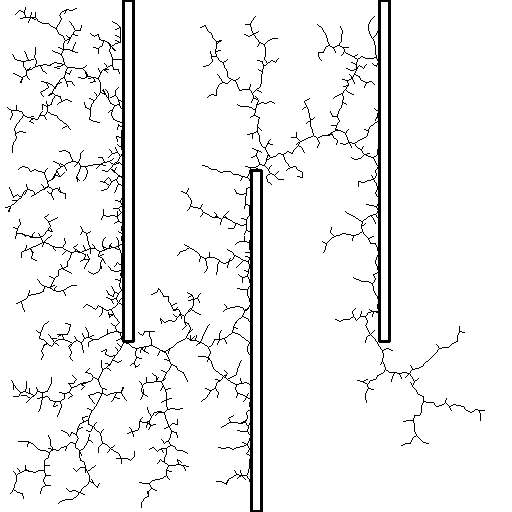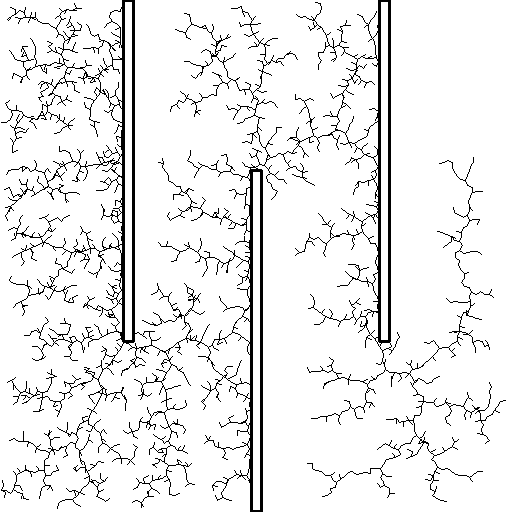
Rapidly exploring random tree ()

[sketch]
- Tools: Python
- Source code: https://github.com/vec2pt/py-sketches
- Links:

import math
import random
from dataclasses import dataclass
from typing import Self
from PIL import Image, ImageDraw
@dataclass
class Node:
"""Node.
Attributes:
x: Node x.
y: Node y.
parent: Node parent.
"""
x: float
y: float
parent: None | Self = None
def __eq__(self, other):
return self.x == other.x and self.y == other.y
@dataclass
class Wall:
"""Simple wall.
Attributes:
x1: Start point x.
y1: Start point y.
x2: End point x.
y2: End point y.
"""
x1: float
y1: float
x2: float
y2: float
def distance(node1: Node, node2: Node) -> float:
"""Distance between two nodes.
Args:
node1: First node.
node2: Second node.
Returns:
Distance.
"""
return math.hypot(node1.x - node2.x, node1.y - node2.y)
def is_intersect(p00, p01, p10, p11) -> bool:
"""Checks whether two line segments intersect.
Args:
p00: Start point of first segment.
p01: End point of first segment.
p10: Start point of second segment.
p11: End point of second segment.
Returns:
True if intersect / False if not.
"""
def orientation(a, b, c):
return (b[0] - a[0]) * (c[1] - a[1]) - (b[1] - a[1]) * (c[0] - a[0])
def on_segment(spt1, spt2, pt):
x_test = min(spt1[0], spt2[0]) <= pt[0] <= max(spt1[0], spt2[0])
y_test = min(spt1[1], spt2[1]) <= pt[1] <= max(spt1[1], spt2[1])
return x_test and y_test
s1 = orientation(p00, p01, p10)
s2 = orientation(p00, p01, p11)
s3 = orientation(p10, p11, p00)
s4 = orientation(p10, p11, p01)
return any(
[
# General
((s1 > 0) != (s2 > 0) and (s3 > 0) != (s4 > 0)),
# Collinearity
(s1 == 0 and on_segment(p00, p01, p10)),
(s2 == 0 and on_segment(p00, p01, p11)),
(s3 == 0 and on_segment(p10, p11, p00)),
(s4 == 0 and on_segment(p10, p11, p01)),
]
)
class RRT:
"""Rapidly exploring random tree (RRT)."""
def __init__(
self,
initial_tree: list[Node],
step_size: float = 5,
walls: list[Wall] | None = None,
allow_self_intersection: bool = True,
size: tuple[int, int] = (512, 512),
) -> None:
"""Rapidly exploring random tree (RRT).
Args:
initial_tree: Initial tree.
step_size: Step size.
walls: List of walls.
allow_self_intersection: Allow self intersection.
size: Size.
"""
self._tree = initial_tree
self.step_size = step_size
self._walls = walls
self._allow_self_intersection = allow_self_intersection
self._size = size
@property
def tree(self):
"""Rapidly exploring random tree."""
return self._tree
def _is_self_intersection(self, node: Node) -> bool:
for n in self._tree:
if n.parent is None or node.parent is None:
continue
if node.parent in (n, n.parent):
continue
a, b, c, d = (
(node.parent.x, node.parent.y),
(node.x, node.y),
(n.parent.x, n.parent.y),
(n.x, n.y),
)
intersect = is_intersect(a, b, c, d)
if intersect:
return True
return False
def _is_collision(self, node: Node) -> bool:
if node.parent is None:
raise Exception(
"Collision checking is not possible for a node without a parent."
)
if self._walls:
for wall in self._walls:
a, b, c, d = (
(node.parent.x, node.parent.y),
(node.x, node.y),
(wall.x1, wall.y1),
(wall.x2, wall.y2),
)
intersect = is_intersect(a, b, c, d)
if intersect:
return True
return False
def __iter__(self) -> Self:
return self
def __next__(self) -> Node | None:
random_node = Node(
random.uniform(0, self._size[0]), random.uniform(0, self._size[1])
)
nearest = min(self._tree, key=lambda n: distance(n, random_node))
theta = math.atan2(random_node.y - nearest.y, random_node.x - nearest.x)
new_node = Node(
nearest.x + self.step_size * math.cos(theta),
nearest.y + self.step_size * math.sin(theta),
parent=nearest,
)
if self._is_collision(new_node):
return
if not self._allow_self_intersection and self._is_self_intersection(
new_node
):
return
self._tree.append(new_node)
return new_node
def plot(self) -> Image.Image:
im = Image.new("L", self._size, 255)
draw = ImageDraw.Draw(im)
for node in self._tree:
if node.parent:
draw.line(
(node.x, node.y, node.parent.x, node.parent.y), fill=0
)
if self._walls:
for w in self._walls:
draw.line((w.x1, w.y1, w.x2, w.y2), fill=0, width=3)
return im
if __name__ == "__main__":
width, height = 512, 512
rrt = RRT(initial_tree=[Node(width / 2, height / 2)], size=(width, height))
steps = 5000
for i in range(steps):
_ = next(rrt)
rrt.plot().save("rrt.png")